SDFs (Plane Box and Sphere)

Introduction
SDFs (Signed Distance Functions) are important, especially in ray marching. So I have to learn how most of them are derived. So, I will post blogs for the SDFs that I have studied and implemented in shadertoy. I will use the basic raymarcher that I have implemented for testing these SDFs. This blog is rather simpler because they implement the simplest SDFs. These are:
- Axis-aligned plane
- Sphere
- Box
Axis-Aligned Plane
Getting the distance between a point and an axis-aligned plane is very easy. Let's consider a plane and the normal of that plane points upwards (+y direction). This means that for any point in the 3D space, the distance is just the y component of the point.
float GetDist(vec3 pos)
{
float planeDistance = pos.y;
return planeDistance;
}
So, the plane looks like this with ray marching:

SDF of a plane
Sphere
Sphere is also straightforward. Distance to a sphere is the distance to its center minus the radius of the sphere. So, we calculate it as follows:
float dSphere(vec3 pos, vec3 sphereOrigin, float sphereRadius)
{
return length(pos - sphereOrigin) - sphereRadius;
}
float GetDist(vec3 pos)
{
float sphereDistance = dSphere(pos, vec3(1.0,1.0,-3.0), 1.0);
return sphereDistance;
}
The sphere looks like this when rendered with ray marching:

SDF of a sphere
Box
The SDF of a box is a little bit more complicated but it is still easy to understand. The figure below shows two different points:
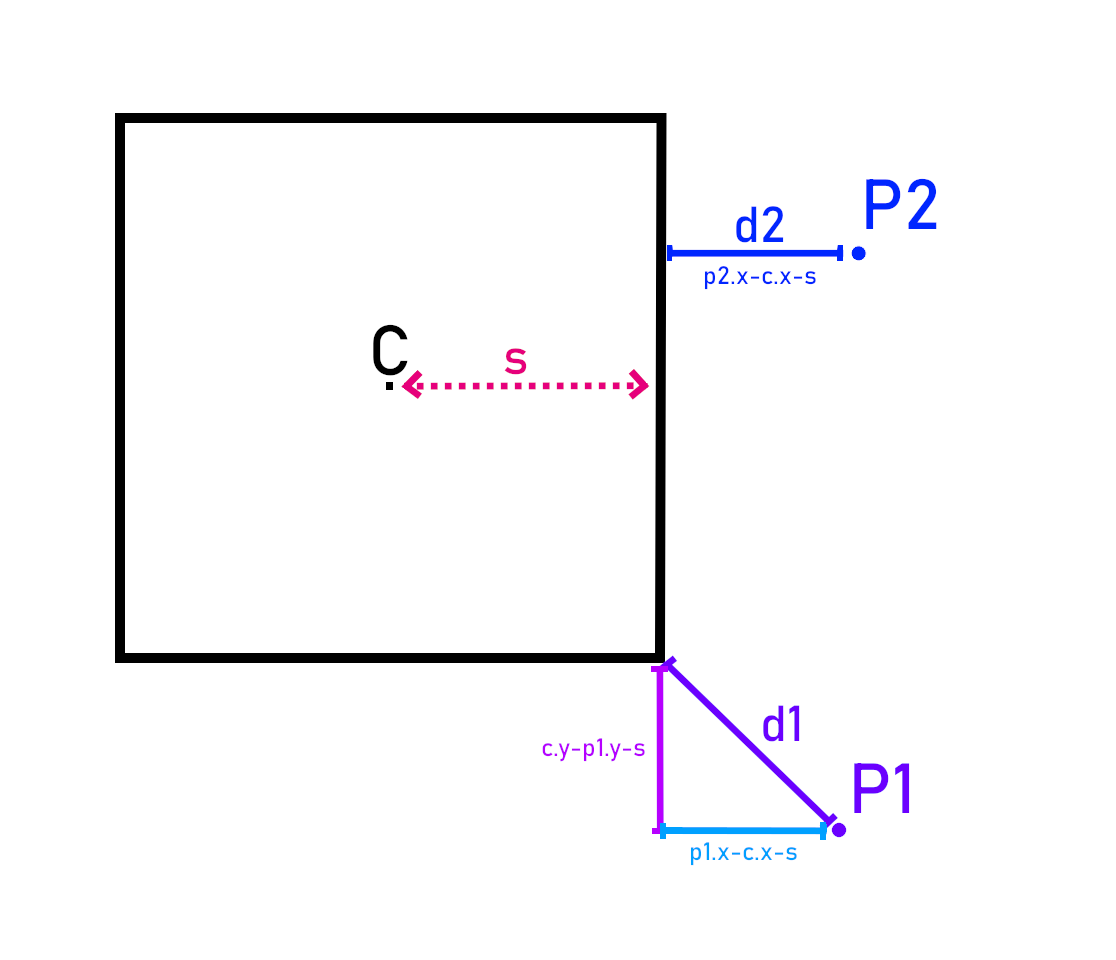
Explanation of box SDF
Here, we have two points:
- P1
- P2
For P1, The nearest point on the box is the corner of the box. So, in this case, we have to find d1 using the Pythagorean theorem:
For P2, it is relatively easier to calculate d2. It is just
In this example, I have deliberately changed the order of operands in substractions, but normally, points may be near different faces of the box. They might be on the left side upper part for example. So, we need to generalize our findings for all points. For that, we can first carry every point to the first quadrant by taking the absolute value of each component of the coordinate. And then, we substract s from what is left. Secondly, we also have to check whether a component is negative. For example, in the figure above, we can see that P2's abs(p_y) - s is negative. So, if that is the case, we make this value zero.
In addition, we also have to take points that are very close to the box surface but inside the box. This is for correcting some rendering artifacts. If the point is directly inside the box, we take the component that is closest to zero and add it to the final length. So, our SDF and its use case become:
float dBox(vec3 p, vec3 s)
{
p = abs(p) - s;
return (length(max(p, 0.0)) + min(max(p.x, max(p.y,p.z)), 0.0));
}
float GetDist(vec3 pos)
{
float boxDistance = dBox(pos, vec3(1.0,1.0,1.0));
return boxDistance;
}
As it is seen above, this can be applied to 3D as well it works fine. The box looks like this when rendered:

SDF of a Box
Conclusion
In this post, I have tried to explain what I have learned while studying basic SDFs.