Smooth Minimum Function

Introduction
While studying SDFs, I have learned that we combine different elements in the scene using min function. But sometimes, we might want to blend those objects for artistic purposes. I saw that they do it a lot with volumetric rendering.
I have learned how it is implemented by reading the article of Inigo Quilez about smooth min function. In this article, he gives implementations of different smooth min functions and clearly explains how they work. He also explains the derivation of polynomial smooth min 2 function that he gave as an example. To learn better, I would like to explain what I understood and document it in this blog post. This topic has already been explained by lots of programmers but here, my intention is only to document what I have understood.
Polynomial Smooth Min
In the article, the code for the smooth minimum function is the following:
float smin( float a, float b, float k )
{
float h = max( k-abs(a-b), 0.0 )/k;
return min( a, b ) - h*h*k*(1.0/4.0);
}
So, in this code, a and b are some function values and k determines how smooth their minimum will be. For example, let's think like this:
- let a be f(x)
- let b be g(x)
These two functions look like the following:
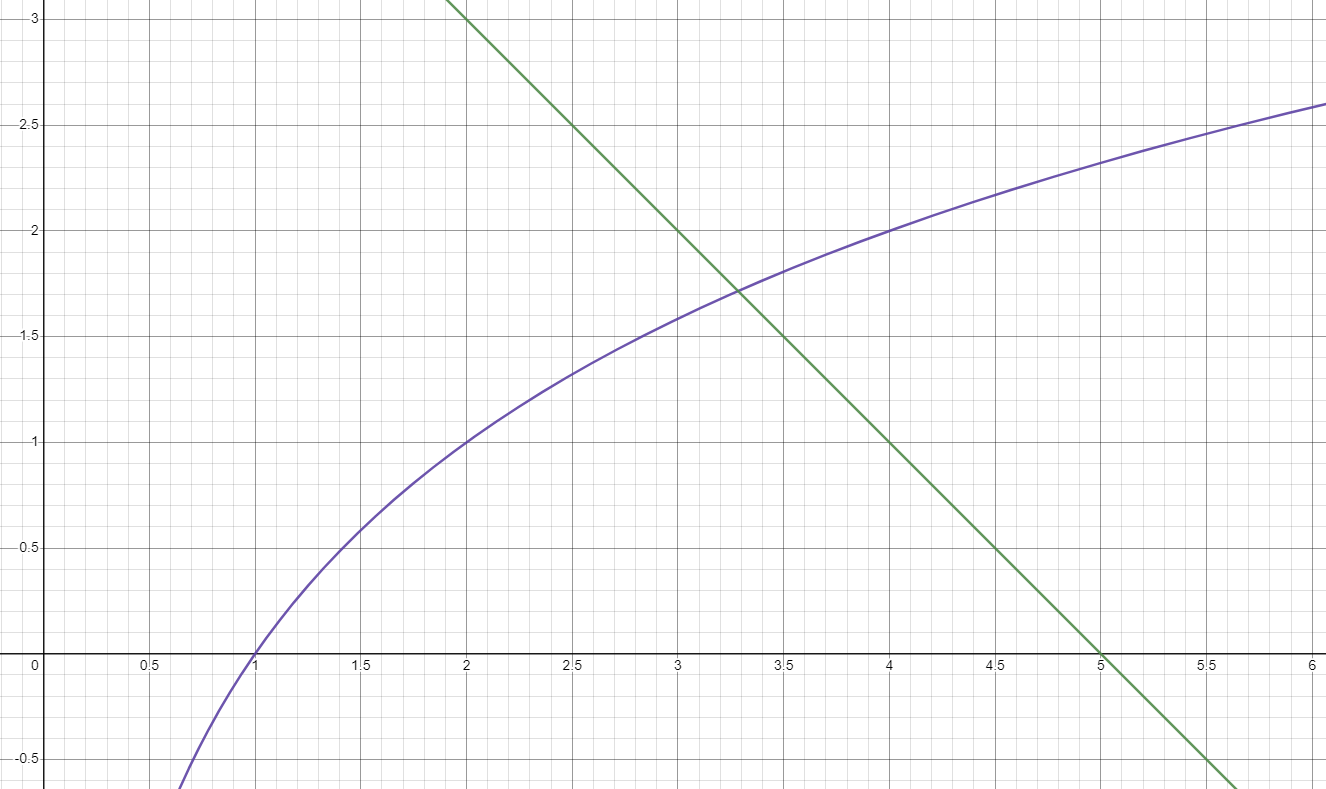
f(x) and g(x)
In the above figure, we can see what f(x) (purple) and g(x) (green) look like. If we want to take the minimum of these two functions, we would get the function below:
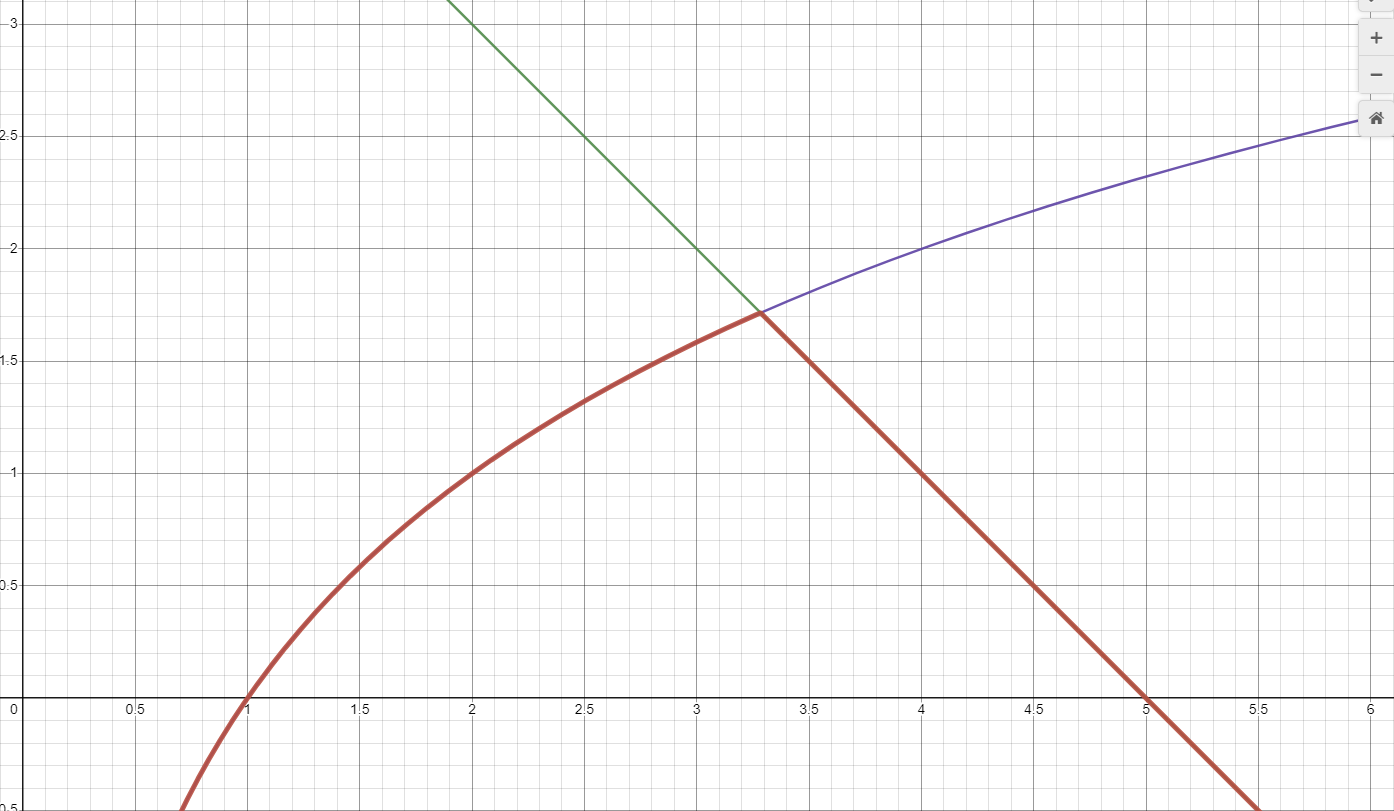
min(f(x), g(x))
We see that the minimum of these two functions is the red curve. This is the ordinary minimum function. But, if we look closely at the intersection point, we see that the transition from left to right is not smooth. According to what I understood, this means that the first and second derivatives of the curve right at the left and the right of the intersection point are not equal. If we want smoothness, they have to be equal.
So, we have to subtract another function from the min(f(x), g(x)) we can name it w(x,k). This function has its peaks at the intersection points of both functions and values start decreasing while moving away from the intersection point. In the article, Inigo Quilez says that w is:
In the equation above, we see that there is another function called h. This function is associated with the absolute value of the difference between both functions. Moreover, we see k which is the smoothness factor. Higher the k value, w(x,k) increases so intersection points are smoothed even further. h function formula is like the following:
And let's look at h visually:
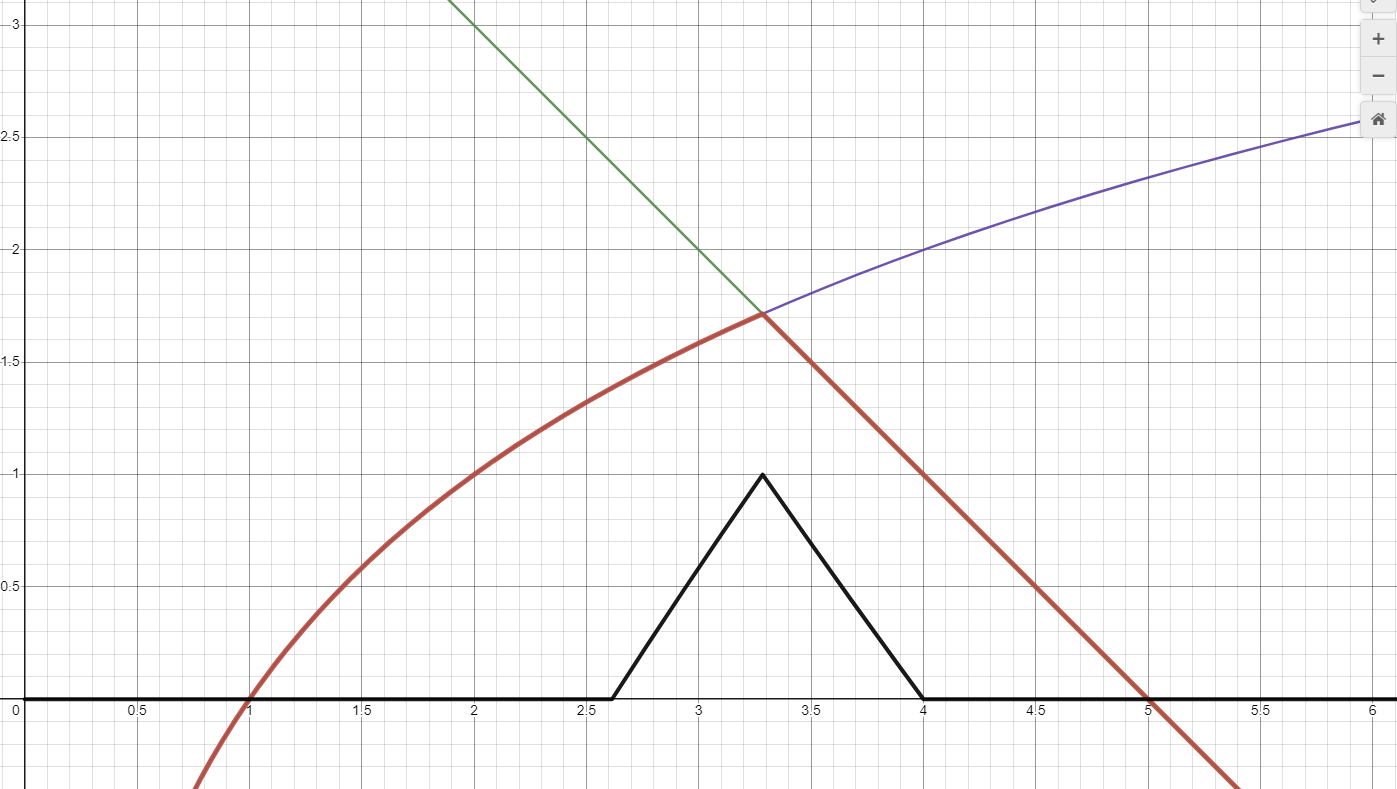
h(x,k)
As it is seen, values of h are clamped between 0 and 1. As k grows, the triangular shape we see here becomes wider, so we get a smoother-looking minimum. The two (left and right) edges of this triangular shape determine where smoothing starts.
And let's now look at the w(x,k) function its formula was
For n=2, let's look at what smoothed-min looks like:
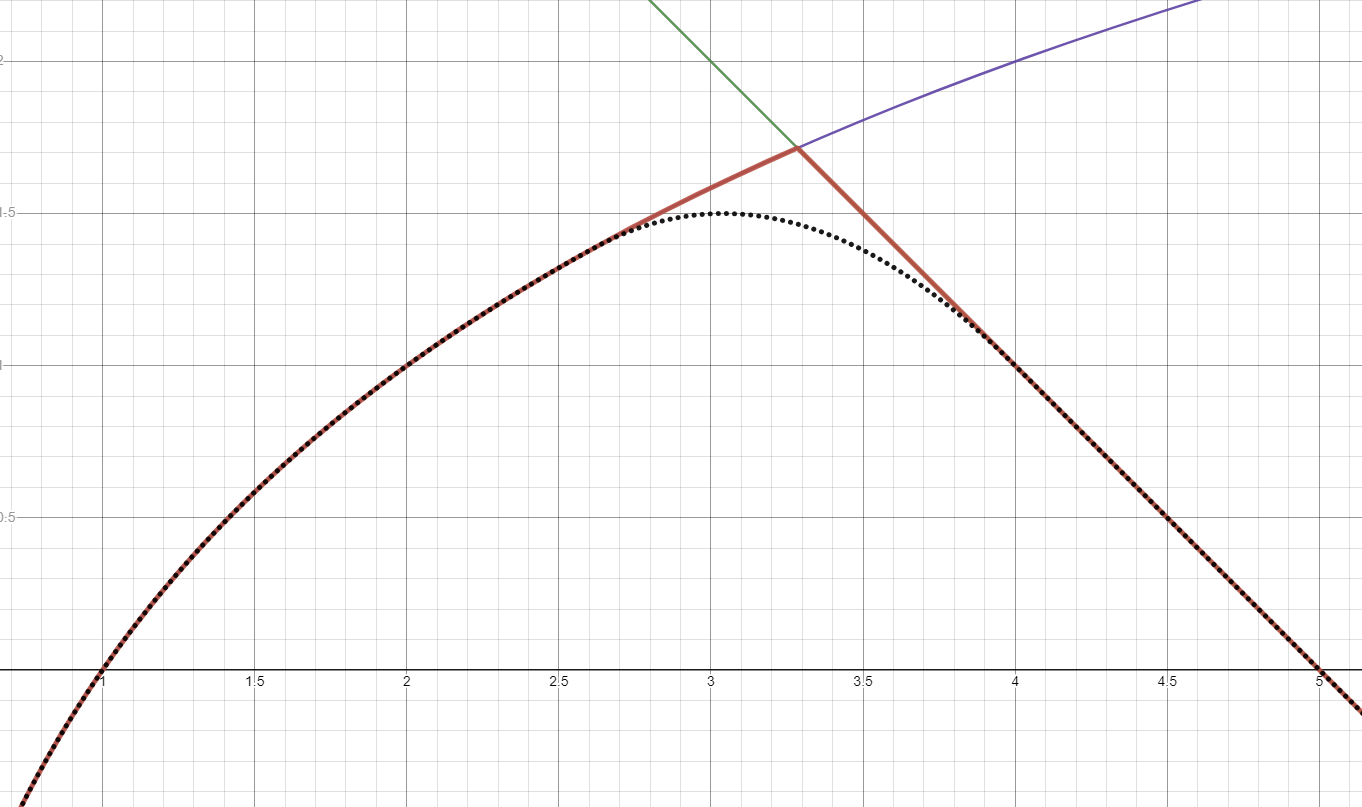
smooth-min
The curve with black dots shows that we have now a smooth min. But why do we have k/2.0*n as the denominator? This comes from the derivates of the left and right parts of the min function. In the article, Inigo Quilez divides w(x,k) function to two parts left and right. He calls them wl(x,k) and wr(x,k). They are divided because of h(x,k) function. Because of the absolute value in h. For explanation, let's write wl(x,k) and wr(x,k) like the following:
So, we have to find s here. And we need to check the equation below. To ensure continuity, derivatives must be equal to each other when coming from both sides of the intersection point:
Here, c point is the intersection point of the two functions. So when x=c, f(x) - g(x) will always be zero. Let's take the derivatives and look again:
If we plug those into the equation, we have this:
So, smooth min becomes
This is what it looks like if we use it on SDFs:

smooth-min
If we had used the ordinary minimum function instead of smooth min, two objects would look like the following:

ordinary minimum function
Conclusion
So, this is what I understood from smooth minimum function. It looks like a very powerful tool.