SDFs (Torus Capsule and Cylinder)

Introduction
In the previous blog, I explained what I understood on how to implement Axis-Aligned Plane, Sphere and Box. This time, I am looking at:
- Torus
- Capsule
- Cylinder
Torus
Torus is relatively simpler than the other two here. We have two radii to work with. One is the radius of the circle which is the shape we see when we look at the torus from above. The other radius is the radius of the tube which goes along the circumference of the circle that I explained in the previous sentence. The closest point on the surface of a torus to an arbitrary point can be seen in this figure:
Closest Distance to a Torus
We assume that the torus sits on the xz plane where the center is on the origin. We can change orientation and position by manipulating the input point we give. So, we have to take the shadow of the point on xz plane and calculate the distance to the small circle's center. And then, by using the Pythagorean theorem, we can easily calculate the length between points P and C2.
So this way, we obtain a distance function to a torus object. It looks like this with ray marching:

Torus object
Its SDF code in shadertoy looks like the following. It does the calculations explained above:
float Torus(vec3 p, vec2 r) {
float x = length(p.xz)-r.x;
return length(vec2(x, p.y))-r.y;
}
Capsule
Finding the distance to a capsule is also straightforward. Let's think about a capsule where the bottom circle's center is C1 and the top circle is C2. In the capsule, C1 is always below C2. There are 3 possibilities:
- Point is above of both C1 and C2
- Point is below of both C1 and C2
- Point is between C1 and C2
Finding distance for the first two situations is easy. We easily find the distance between the point and the circle center (C1 or C2). For the other situation where the point is between C1 and C2, we need to find the point that produces a perpendicular vector to the vector C1 - C2. For this, we find projection using dot products. The idea is shown below:
Closest Distance to a Capsule
So, let's think the point X as a movable point between C1 and C2. We first produce a vector from C1 to P and take the dot product of this vector and the vector from C1 to C2 and divide the whole thing by the multiplication of two vectors' lengths. So, we get the t value. In the end, we also clamp the resulting t value. This gives us a float between 0 and 1. So:
From the equations above, we see that if the first situation is the case, t is 1 and X is equal to C2, for the second situation, it is 0 and X is equal to C1 and for the third one, it is between 0 and 1. The only thing that is left is to find the distance between X and our Point and subtract the radius from the result.
For ray marching, it is coded like this:
float Capsule(vec3 p, float r)
{
vec3 c1 = vec3(0.0, -0.5, 0.0);
vec3 c2 = vec3(0.0, 0.5, 0.0);
vec3 c1c2 = c2-c1;
vec3 c1p = p-c1;
float t = dot(c1c2, c1p) / dot(c1c2, c1c2);
t = clamp(t, 0., 1.);
vec3 x = c1 + t*normalize(c1c2);
return length(p-x)-r;
}
In the code above, since the vector C1C2 is already normalized, we don't even need to normalize it while calculating x. But I'm keeping it anyways. The resulting capsule looks like the following:

Capsule Object
Cylinder
The logic behind the cylinder's SDF is very similar to the Capsule. We just need to explain where the closest point on the cylinder is the top or bottom parts (bases). Just like the capsule we still have three possibilities:
- Point is above of both C1 and C2
- Point is below of both C1 and C2
- Point is between C1 and C2
The image below explains the situation. If first or second possibilities are the case, we have to somehow find y, x values and compute the distance using the Pythagorean theorem. If the point is directly below the bottom or top of two circle bases of the cylinder, then we don't even need x value, only y value gives the distance.
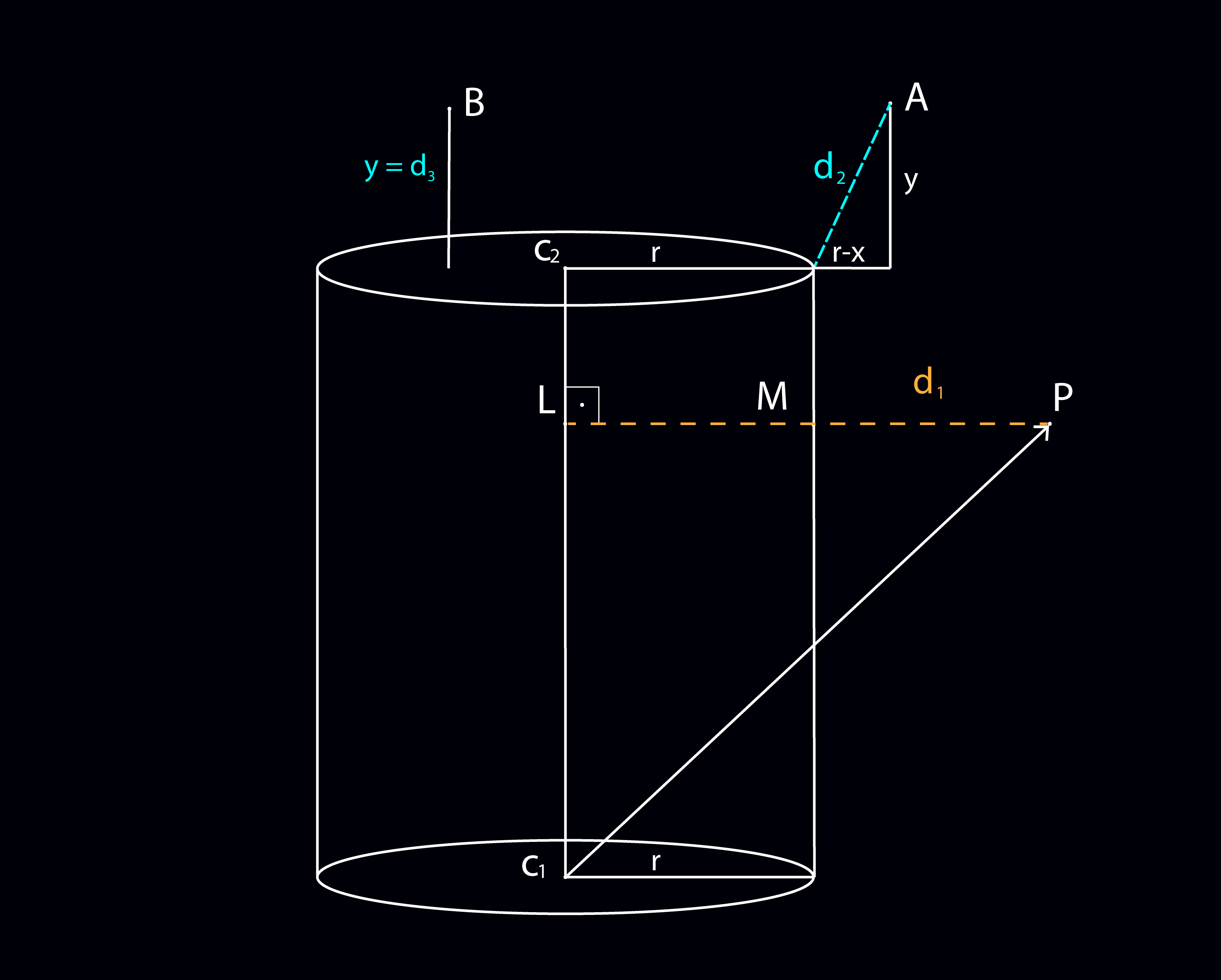
Closest distance to a Cylinder
The logic is the same with a capsule, but we need to find a way to efficiently compute the y value from the values we get. So just like in the cylinder, we have to compute a t value to get the x:
Now, we can efficiently get the y value. We can do it as follows (c1 is the vec3 point for the bottom base and c2 is the vec3 point for the top base):
This way, we get the SDF of a cylinder. Lastly, we also have to add an interior distance if the point is very close to the surface but inside the cylinder. This trick prevent some artifacts of ray marching:
float interiorDistance = min(max(x,y), 0.0);
The full code is the following:
float sdCylinder(vec3 p, float r)
{
vec3 c1 = vec3(0.0, -0.5, 0.0);
vec3 c2 = vec3(0.0, 0.5, 0.0);
vec3 c1c2 = c2 - c1;
vec3 c1p = p - c1;
float t = dot(c1c2, c1p) / dot(c1c2, c1c2);
vec3 c = c1 + t*c1c2;
float x = length(p-c) - r;
float y = (abs(t - 0.5) - 0.5) * length(c1c2);
float e = length(max(vec2(x,y), 0.0));
// Interior Distance
float i = min(max(x,y), 0.0);
return e+i;
}
The resulting cylinder looks like the following in shadertoy:

Cylinder Object